Estimate transfer function models by Least Squares.

Source: R/armax.ls.fit.R

Calibrate unit hydrograph transfer function models (armax or expuh) using Least Squares with prefiltering.

armax.ls.fit(
  DATA,
  order = hydromad.getOption("order"),
  delay = hydromad.getOption("delay"),
  prefilter = hydromad.getOption("prefilter"),
  warmup = hydromad.getOption("warmup"),
  normalise = FALSE,
  fixed.ar = NULL,
  weights = NULL,
  initX = TRUE,
  na.action = na.pass,
  trace = hydromad.getOption("trace")
)

Arguments

DATA

a ts-like object with named columns:

list("U")

observed input time series.

list("Q")

observed output time series.

order

the transfer function order. See armax.

delay

delay (lag time / dead time) in number of time steps. If missing, this will be estimated from the cross correlation function.

prefilter

placeholder

warmup

placeholder

normalise

placeholder

fixed.ar

placeholder

weights

placeholder

initX

placeholder

na.action

placeholder

trace

placeholder (i.e. negative or imaginary poles) are detected.

Value

a tf object, which is a list with components

coefficients

the fitted parameter values.

fitted.values

the fitted values.

residuals

the residuals.

delay

the (possibly fitted) delay time.

Details

In normal usage, one would not call these functions directly, but rather specify the routing fitting method for a hydromad model using that function's rfit argument. E.g. to specify fitting an expuh routing model by least squares one could write

hydromad(..., routing = "expuh", rfit = "ls")

which uses the default order, hydromad.getOption("order"), or

hydromad(..., routing = "expuh", rfit = list("ls", order = c(2,1))).

References

Jakeman

Author

Felix Andrews felix@nfrac.org

Examples


U <- ts(c(0, 0, 0, 1, rep(0, 30), 1, rep(0, 20)))
Y <- expuh.sim(lag(U, -1), tau_s = 10, tau_q = 2, v_s = 0.5, v_3 = 0.1)
set.seed(0)
Yh <- Y * rnorm(Y, mean = 1, sd = 0.2)
fit1 <- armax.ls.fit(ts.union(U = U, Q = Yh),
  order = c(2, 2), warmup = 0
)
fit1
#> 
#> Unit Hydrograph / Linear Transfer Function
#> 
#> Call:
#> armax.ls.fit(DATA = ts.union(U = U, Q = Yh), order = c(2, 2), 
#>     warmup = 0)
#> 
#> Order: (n=2, m=2)  Delay: 1
#> ARMAX Parameters:
#>       a_1        a_2        b_0        b_1        b_2  
#>  1.249502  -0.324895   0.349207  -0.266033  -0.002811  
#> Exponential component parameters:
#>     tau_s      tau_q        v_s        v_q        v_3  
#>  7.859172   1.002996   0.625975   0.448592  -0.008654  
#> TF Structure: S + Q + inst. (three in parallel)
#>     Poles:0.369, 0.8805
#> 
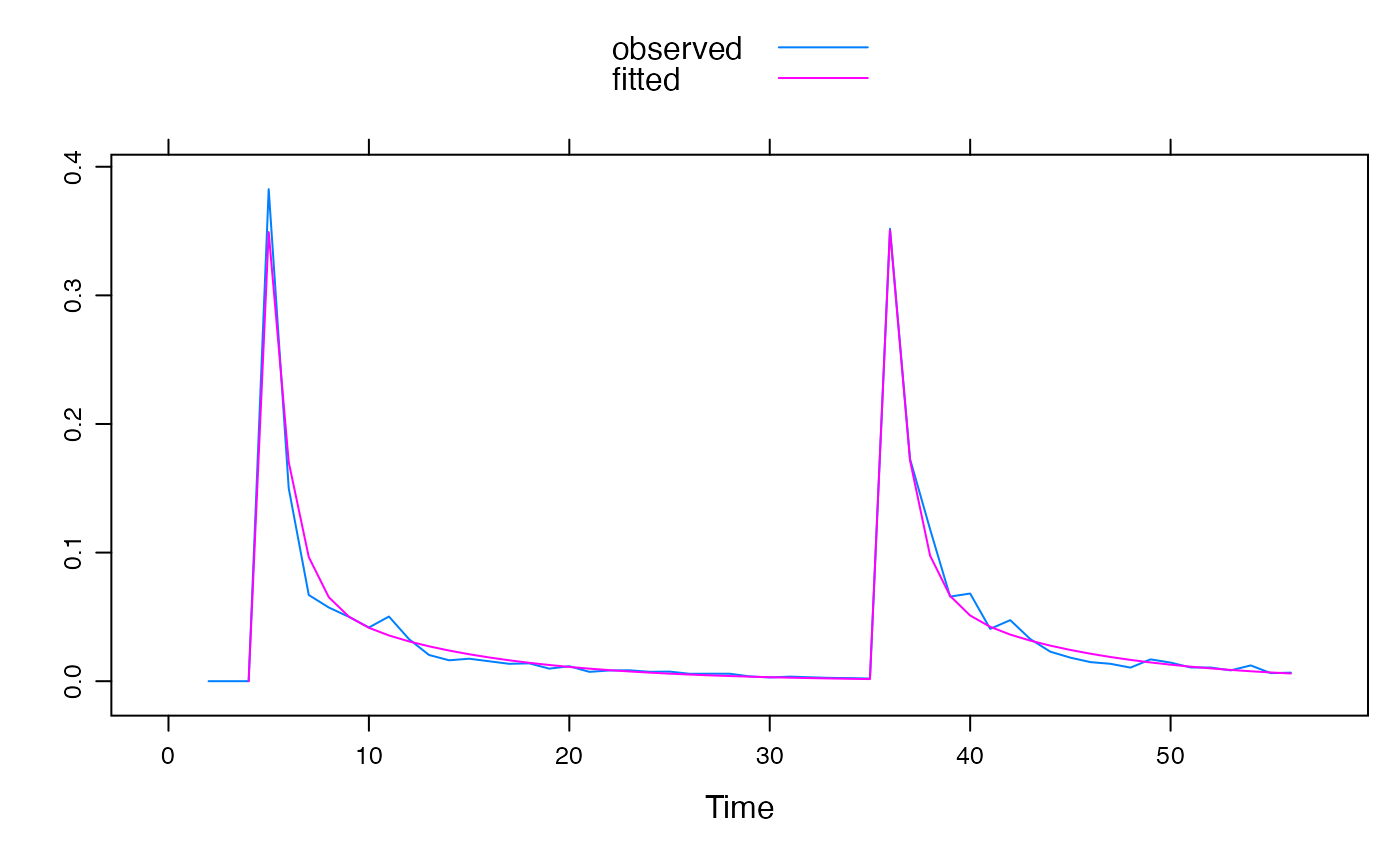
xyplot(ts.union(observed = Yh, fitted = fitted(fit1)),
  superpose = TRUE
)