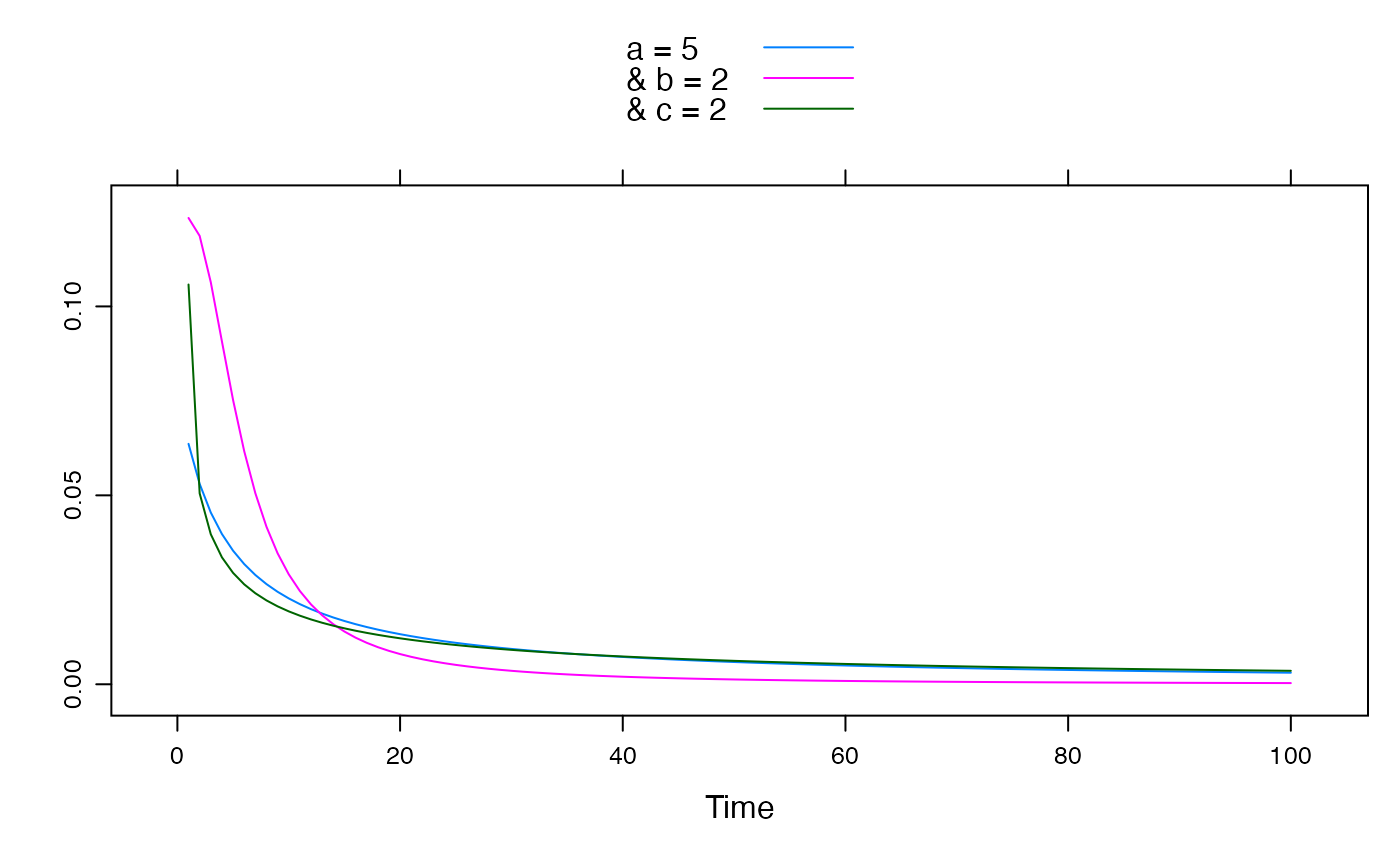
A power-law form of unit hydrograph (transfer function).
powuh.sim(
U,
delay = 0,
a = 1,
b = 1,
c = 1,
init = 0,
uhsteps = 100,
na.action = na.pass,
epsilon = hydromad.getOption("sim.epsilon")
)Arguments
- U
input time series.
- delay
lag (dead time) between input and response, in time steps.
- a
the time for flow to drop by half after a peak, if
c = 1. See Details.- b
persistence of the flow response; defines the recession curve tail.
- c
curvature at half-peak point.
- init
initial flow value(s) used in convolution filter.
- uhsteps
number of time steps to use in approximating the unit hydrograph convolution filter.
- na.action
function to remove missing values, e.g.
na.omit.- epsilon
values smaller than this will be set to zero.
Value
the model output as a ts object, with the same
dimensions and time window as the input U.
Details
The power law form of the unit hydrograph is:
$$H = 1 / (1 + (t/a)^{b/c}) ^ c$$
where H is the fraction of peak flow, t is the time since peak, and a, b and c are parameters.
From Croke (2006):
Parameter a is the value of t (time since peak) at which the ordinate of the asymptote \((t/a)^(-b)\) has a value of 1, b determines the persistence of the flow response and c defines the shape of the response curve near its peak. The c parameter appears twice in order to reduce interaction between the b and c parameters (in this form, the c parameter only influences the curvature near t = a, and doesn't influence the asymptote, which is determined solely by the b parameter). The time for H to decrease to 0.5 is \(a(2^(1/c) - 1)^(c/b)\). While this is a three parameter model, for \(t >> a\) only the b parameter is significant. Since the value of the a parameter is typically significantly less than one (see Table 1) the recession curve can be written as
$$H = (t_r / t)^b$$
where \(t_r\) is some reference time (\(t_r >> a\)) at which the hydrograph profile has been normalized. Thus the remaining two parameters (a and c) only influence the response curve near the event peak, and [the equation above] can be taken as a single parameter recession model.
References
Croke, B.F.W. (2006). A technique for deriving an average event unit hydrograph from streamflow-only data for ephemeral quick-flow-dominant catchments. Advances in Water Resources 29, pp. 493--502.