Simple Wetland Inundation Model using Poweroids

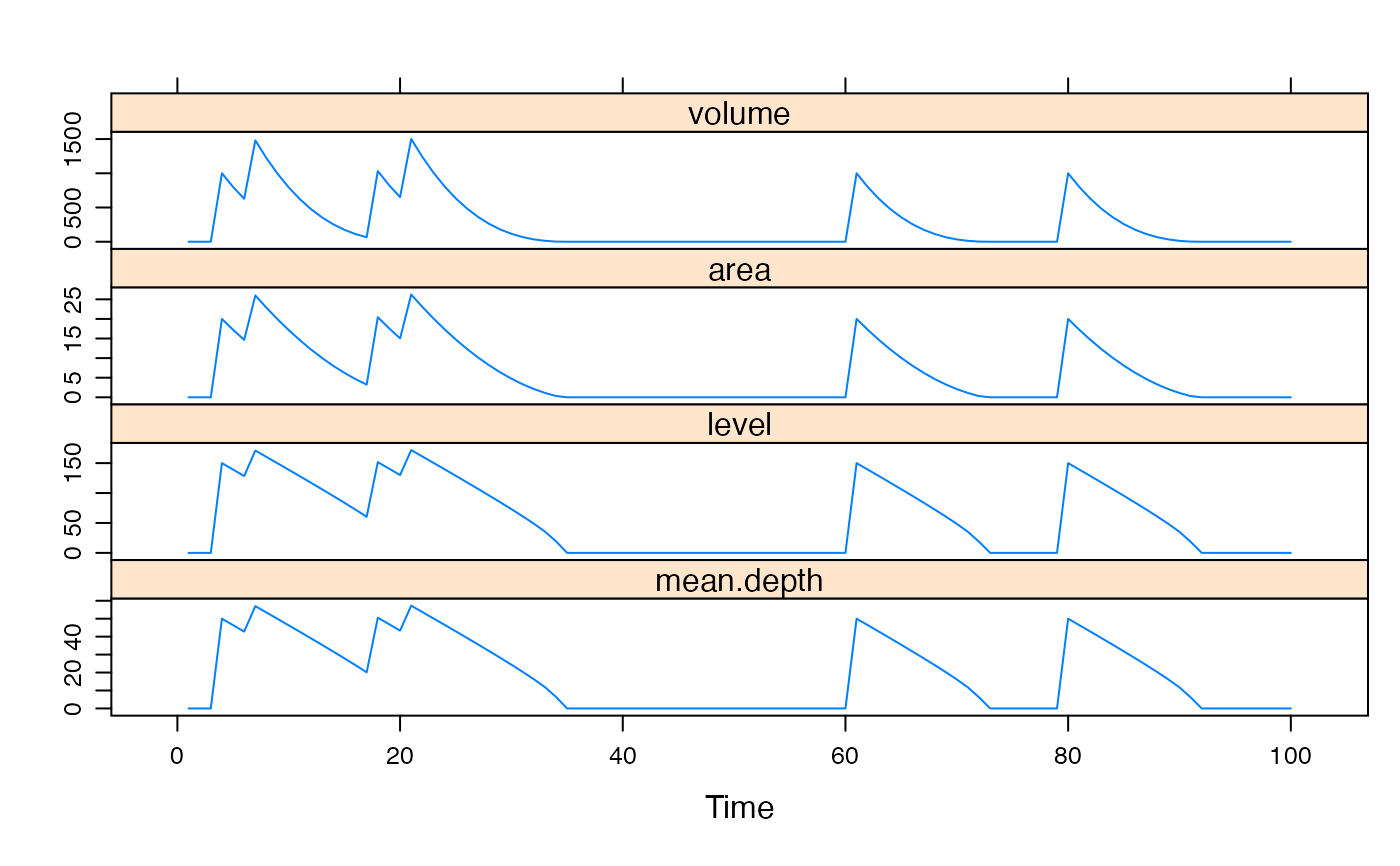
Model flood area / duration / depth in wetlands.

swimp(
  flow.ML,
  thresh = 0,
  alpha,
  beta,
  E.mm = 0,
  P.mm = 0,
  Ksat.mm.day = 0,
  e = 0.2,
  g = 140,
  Hmax = 2000,
  Amax = 10000,
  porosity = 0.2,
  M_0 = Hmax * porosity,
  V_0 = 0,
  drainage = 0,
  drainLevel = 0
)

Arguments

flow.ML

inflow or streamflow in ML per timestep.

thresh

a threshold for flow.ML, such that only flow above this value enters the wetland.

alpha, beta

parameters defining the shape of the wetland. See poweroid.

E.mm, P.mm

potential evapo-transpiration and precipitation in mm per timestep.

Ksat.mm.day

Saturated hydraulic conductivity in mm per timestep, relative to a reference pressure of 10cm. If this is 0, the wetland surface water is isolated from the surrounding water table, i.e. there is no infiltration nor discharge.

e

Placeholder

g

stress threshold in terms of Catchment Moisture Deficit (mm), as in the IHACRES CMD model, where g = f * d. See IHACRES.CMD.model.

Hmax

Placeholder

Amax

Placeholder

porosity

effective porosity of the soil.

M_0

initial value of Catchment Moisture Deficit, mm.

V_0

initial volume of surface water in wetland, ML.

drainage

drainage rate as a proportion of volume above drainLevel per timestep.

drainLevel

water level (millimetres from base) above which drainage occurs.

Value

a zoo object (time series object).

References

...

See also

poweroid, convertFlow

Author

Felix Andrews felix@nfrac.org

Examples

## assume Q is inflow in ML/day
set.seed(1)
Q <- rpois(100, lambda = 0.1) * 1000
## assume depth distribution follows a cone, i.e. beta = 1
## estimate alpha given known area vs volume
## lets say a volume of 1000 ML corresponds to area 20 km^2
alpha <- poweroid(V = 1000, A = 20, beta = 1)$alpha
flood <- swimp(Q, alpha = alpha, beta = 1, E.mm = 10)
head(flood, 20)
#>        volume      area     level mean.depth
#> 1     0.00000  0.000000   0.00000    0.00000
#> 2     0.00000  0.000000   0.00000    0.00000
#> 3     0.00000  0.000000   0.00000    0.00000
#> 4  1000.00000 20.000000 150.00000   50.00000
#> 5   800.00000 17.235478 139.24767   46.41589
#> 6   627.64522 14.661311 128.42887   42.80962
#> 7  1481.03211 25.986013 170.98030   56.99343
#> 8  1221.17199 22.849738 160.33077   53.44359
#> 9   992.67461 19.902208 149.63283   49.87761
#> 10  793.65252 17.144188 138.87841   46.29280
#> 11  622.21064 14.576557 128.05712   42.68571
#> 12  476.44507 12.200339 117.15537   39.05179
#> 13  354.44168 10.016743 106.15477   35.38492
#> 14  254.27426  8.027216  95.02956   31.67652
#> 15  174.00210  6.233515  83.74189   27.91396
#> 16  111.66695  4.637812  72.23253   24.07751
#> 17   65.28884  3.242818  60.40009   20.13336
#> 18 1032.86065 20.435777 151.62536   50.54179
#> 19  828.50289 17.642468 140.88214   46.96071
#> 20  652.07820 15.039375 130.07420   43.35807
xyplot(flood)