An exponential store (linear transfer function) which has a loss term, produces no flow when the store drops below a level, and can therefore model longer-term disconnection of a store from streamflow.
leakyExpStore.sim(x, tau, loss, thres, init = 0, return_components = FALSE)Arguments
- x
input time series.
- tau
Time constant for flow from exponential store.
- loss
Constant loss that occurs while the value of the store is greater than
thres. See details.- thres
Trigger level to turn off loss, which can be interpreted as a store capacity.
- init
Initial value of exponential store
- return_components
whether to return store value (G) as well as flow (Q)
Value
the flow time series with the same dimensions and time windows as
the input x. If return_components = TRUE, it will have
multiple columns named G and Q.
Details
Storage is increased by effective rainfall and decreased by flow and losses. $$G[k] = G[k-1] + U[k] - Q[k] - L[k]$$
Flow is proportional to storage $$Q[k] = a G[k], G[k]>0$$ $$Q[k] = 0, otherwise$$
Loss switches off at some threshold, as a piece-wise continuous function. $$L[k] = L, G[k]>T+L (with T<=0)$$ $$L[k] = G[k] - T, T+L > G[k] > T$$ $$L[k] = 0, G[k]<T$$
See also
Examples
U <- ts(c(1, rep(0, 10), 1, rep(0, 20)))
## Without a loss, equivalent to expuh
## Loss threshold has no effect
all.equal(leakyExpStore.sim(U, 5, loss = 0, thres = 0), expuh.sim(U, tau_s = 5))
#> [1] TRUE
## With losses stopping when flow stops, equivalent to expuh with a loss
all.equal(
leakyExpStore.sim(U, 5, loss = 0.1, thres = 0),
expuh.sim(U, tau_s = 5, loss = 0.1)
)
#> [1] TRUE
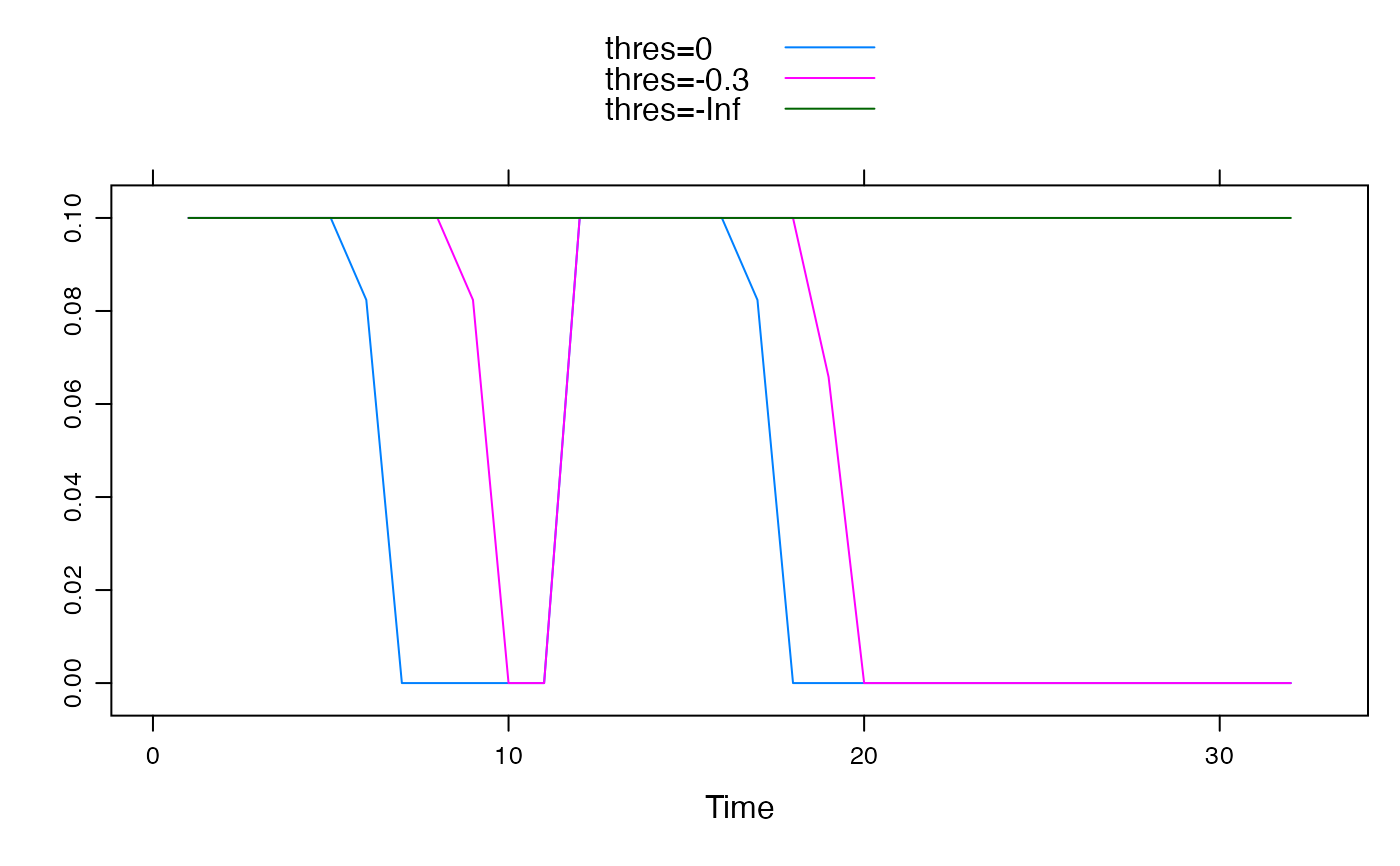
## Plot of unit hydrographs
xyplot(cbind(
"U" = U,
"loss=0" = expuh.sim(U, tau_s = 5),
"loss=0.1 & thres=0" = expuh.sim(U, tau_s = 5, loss = 0.1),
"loss=0.1 & thres=-0.3" = leakyExpStore.sim(U, 5, loss = 0.1, thres = -0.3),
"loss=0.1 & thres=-Inf" = leakyExpStore.sim(U, 5, loss = 0.1, thres = -Inf)
), superpose = TRUE)
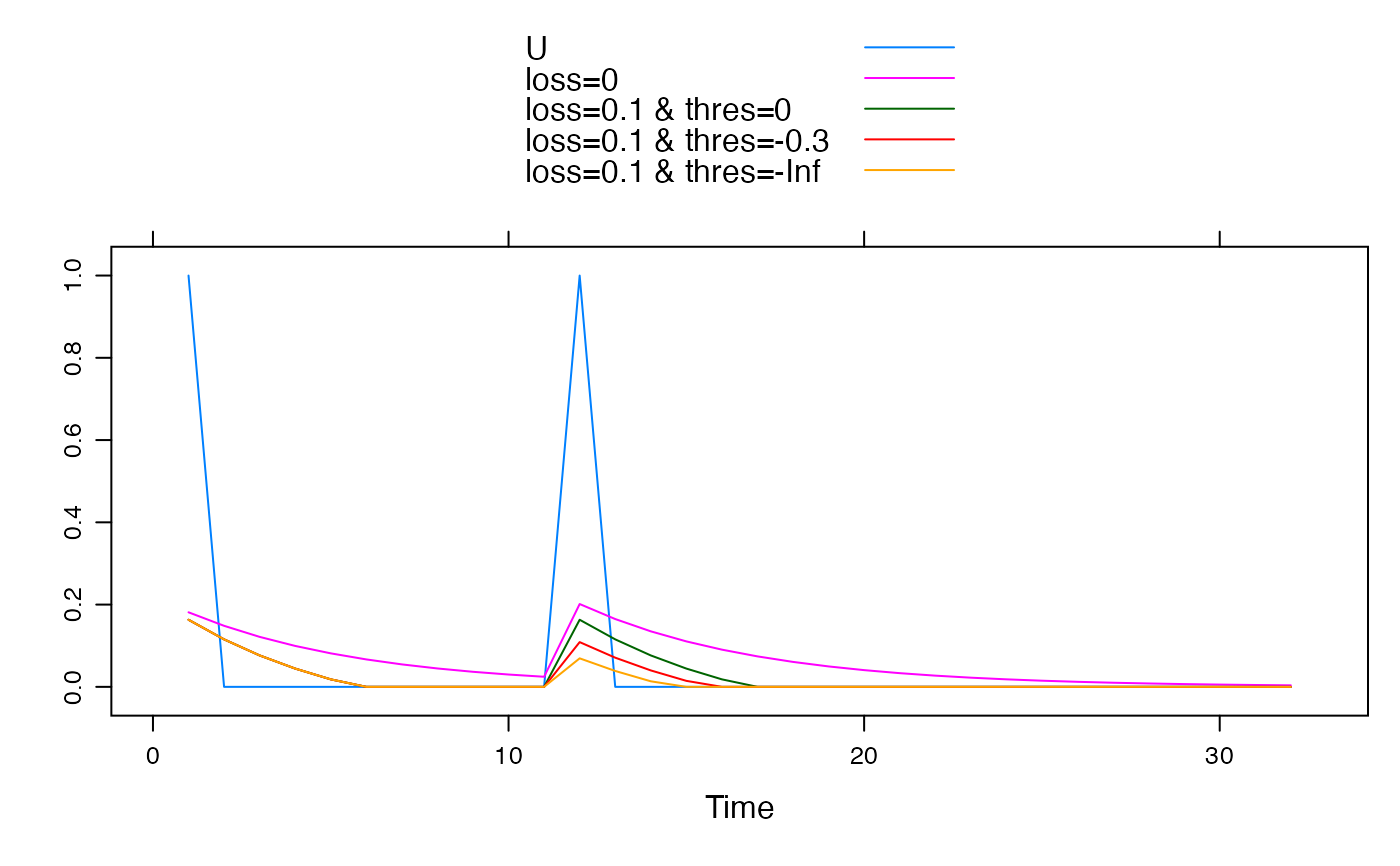 ## Time series plot of value of store
xyplot(cbind(
"thres=0" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = 0,
return_components = TRUE
)[, "G"],
"thres=-0.3" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -0.3,
return_components = TRUE
)[, "G"],
"thres=-Inf" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -Inf,
return_components = TRUE
)[, "G"]
), superpose = TRUE)
## Time series plot of value of store
xyplot(cbind(
"thres=0" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = 0,
return_components = TRUE
)[, "G"],
"thres=-0.3" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -0.3,
return_components = TRUE
)[, "G"],
"thres=-Inf" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -Inf,
return_components = TRUE
)[, "G"]
), superpose = TRUE)
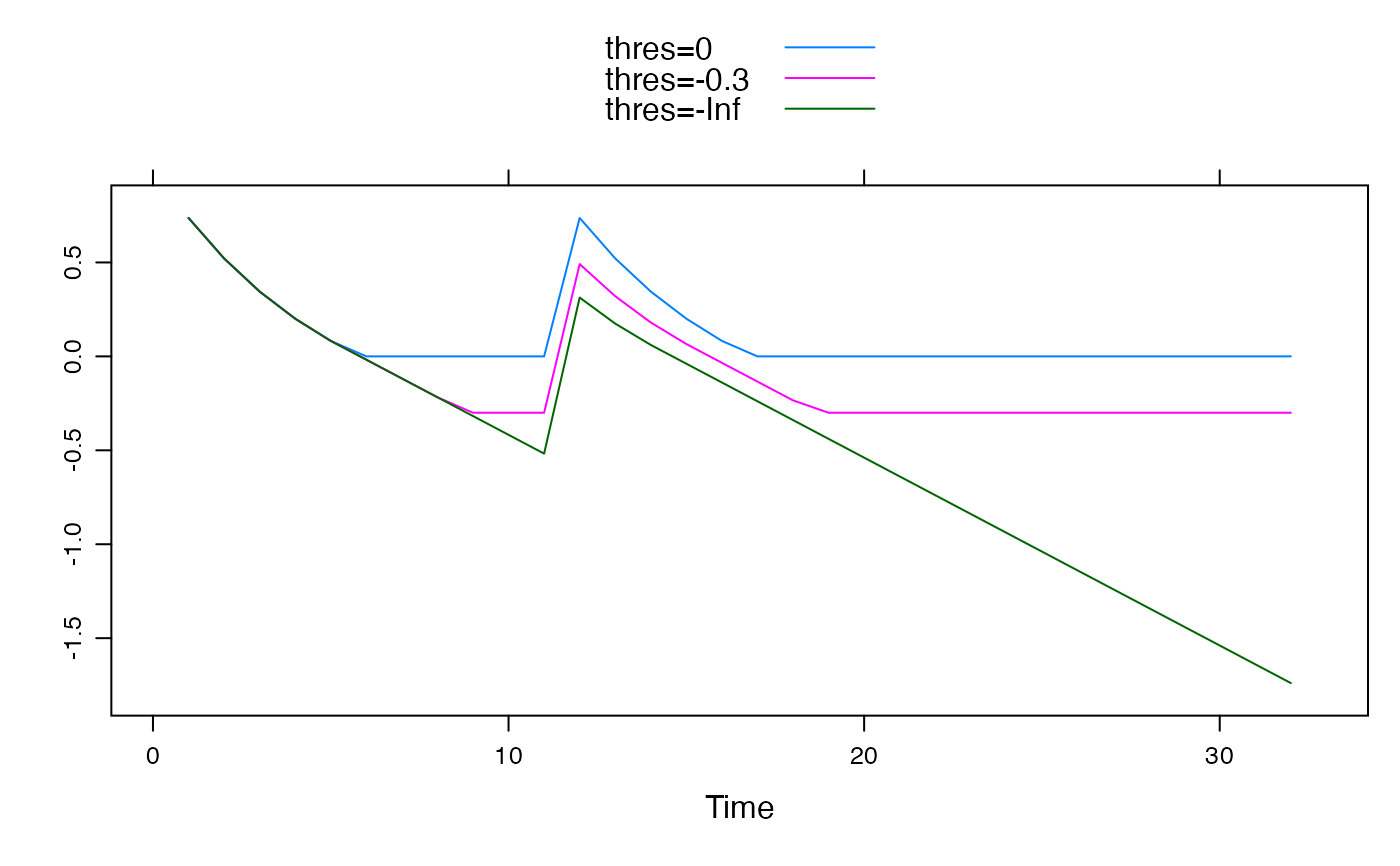 ## Time series of loss
xyplot(cbind(
"thres=0" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = 0,
return_components = TRUE
)[, "L"],
"thres=-0.3" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -0.3,
return_components = TRUE
)[, "L"],
"thres=-Inf" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -Inf,
return_components = TRUE
)[, "L"]
), superpose = TRUE)
## Time series of loss
xyplot(cbind(
"thres=0" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = 0,
return_components = TRUE
)[, "L"],
"thres=-0.3" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -0.3,
return_components = TRUE
)[, "L"],
"thres=-Inf" = leakyExpStore.sim(U, 5,
loss = 0.1, thres = -Inf,
return_components = TRUE
)[, "L"]
), superpose = TRUE)