This is simply an AR(1) recursive filter with a time-varying recession rate.
filter_tv(x, a, init = 0)Arguments
- x
numeric vector or time series.
- a
numeric vector the same length as
x, giving the filter coefficient at each time step.- init
value for
x[0].
Value
a numeric vector or time series, like x.
Note
If there are internal missing values, these are skipped over in the
calculation, maintaining the "state": the value of y[i-1] after any
missing values is the value from just before them. This behaviour is
different from filter, which drops the state back to 0.
See also
Examples
## The non-compiled function is this simple, if there are no NAs:
ftv2 <- function(x, a, init = 0) {
y <- x
y[1] <- x[1] + a[1] * init
for (i in 2:length(x)) {
y[i] <- x[i] + a[i] * y[i - 1]
}
return(y)
}
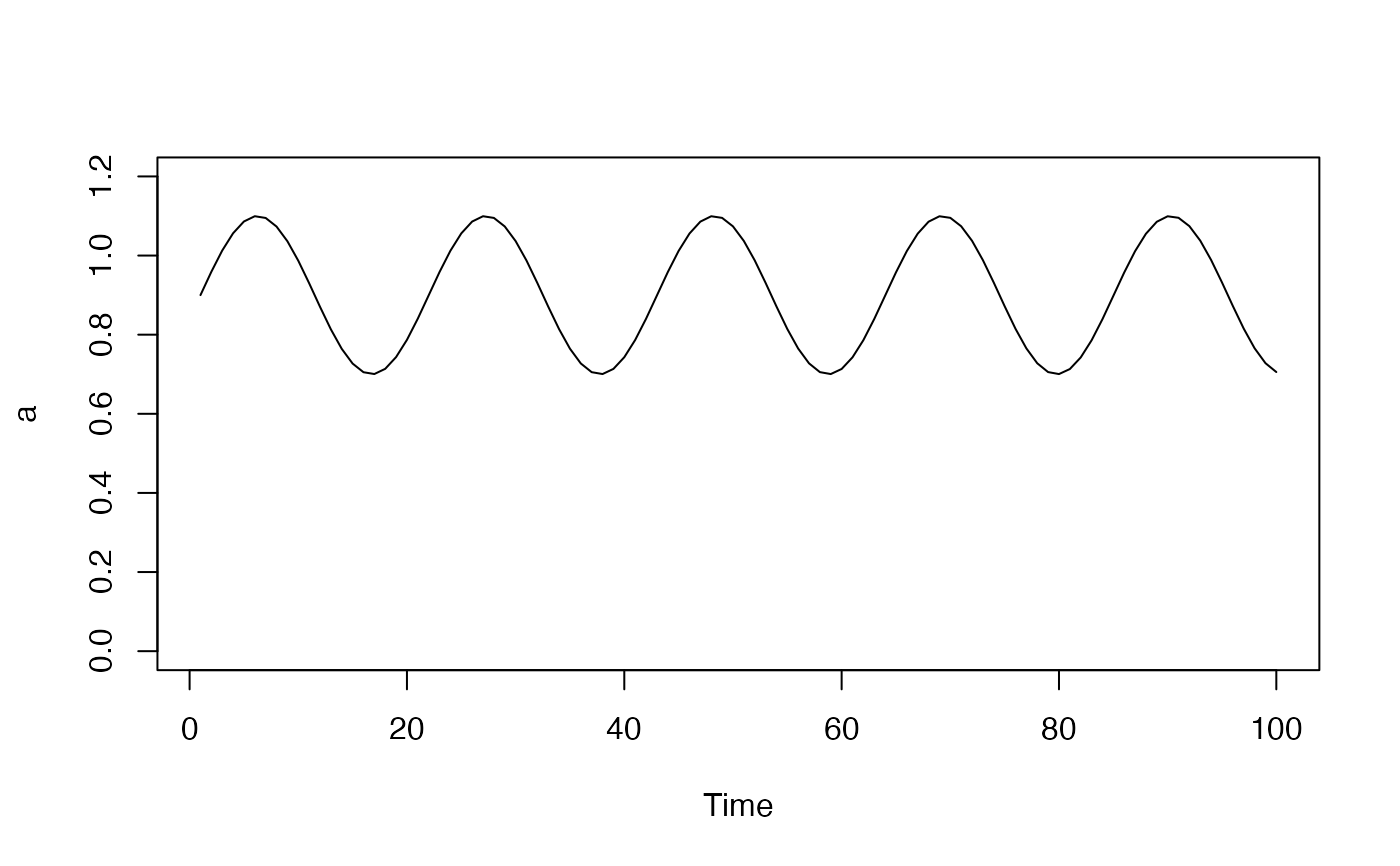
## make a sine wave filter
a <- sin(pi * seq(0, 3 * pi, length = 100)) * 0.2 + 0.9
plot.ts(a, ylim = c(0, 1.2))
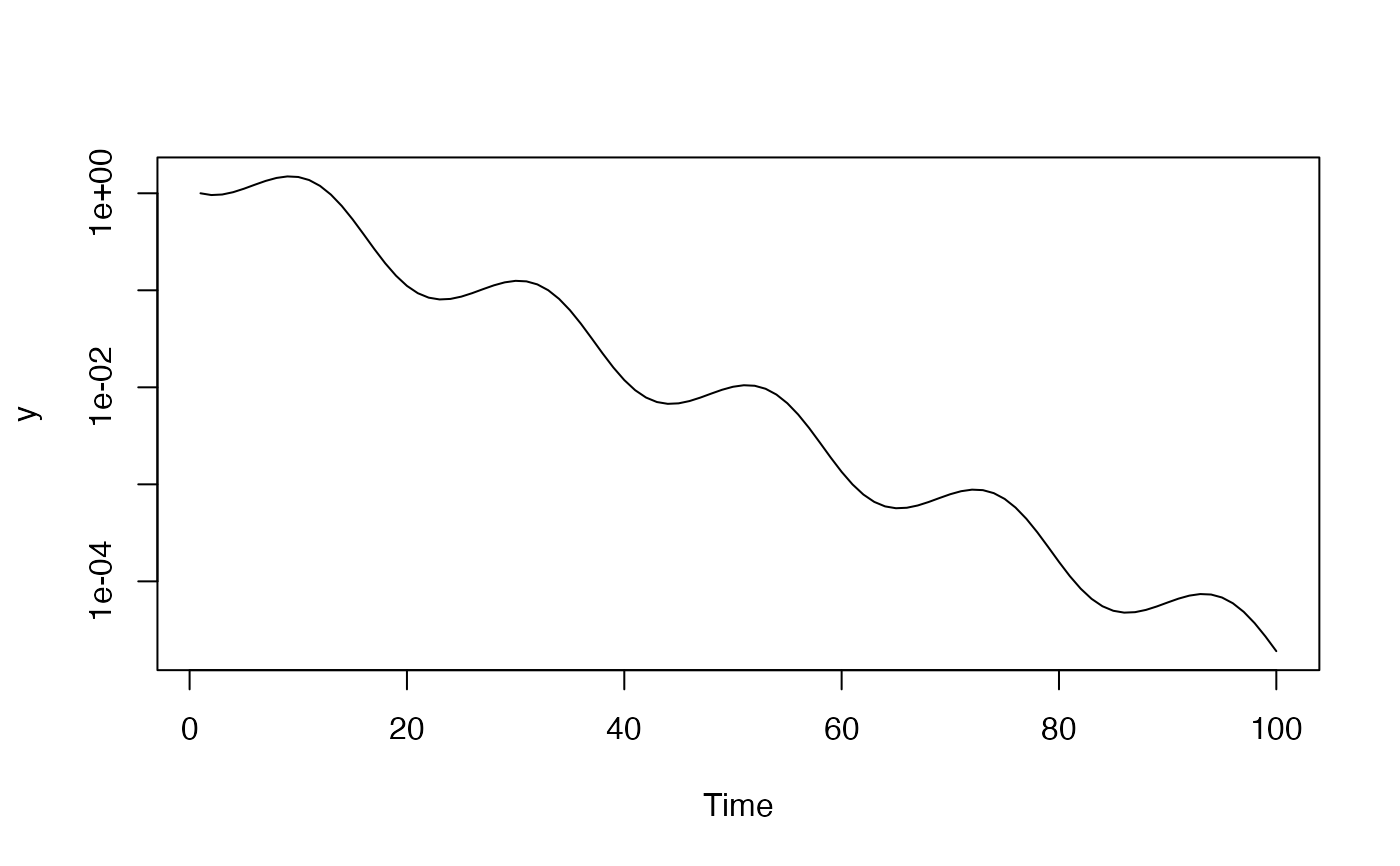
 ## response to a unit impluse
x <- c(1, rep(0, 99))
y <- filter_tv(x, a)
plot.ts(y, log = "y")
## response to a unit impluse
x <- c(1, rep(0, 99))
y <- filter_tv(x, a)
plot.ts(y, log = "y")
 stopifnot(isTRUE(all.equal(y, ftv2(x, a))))
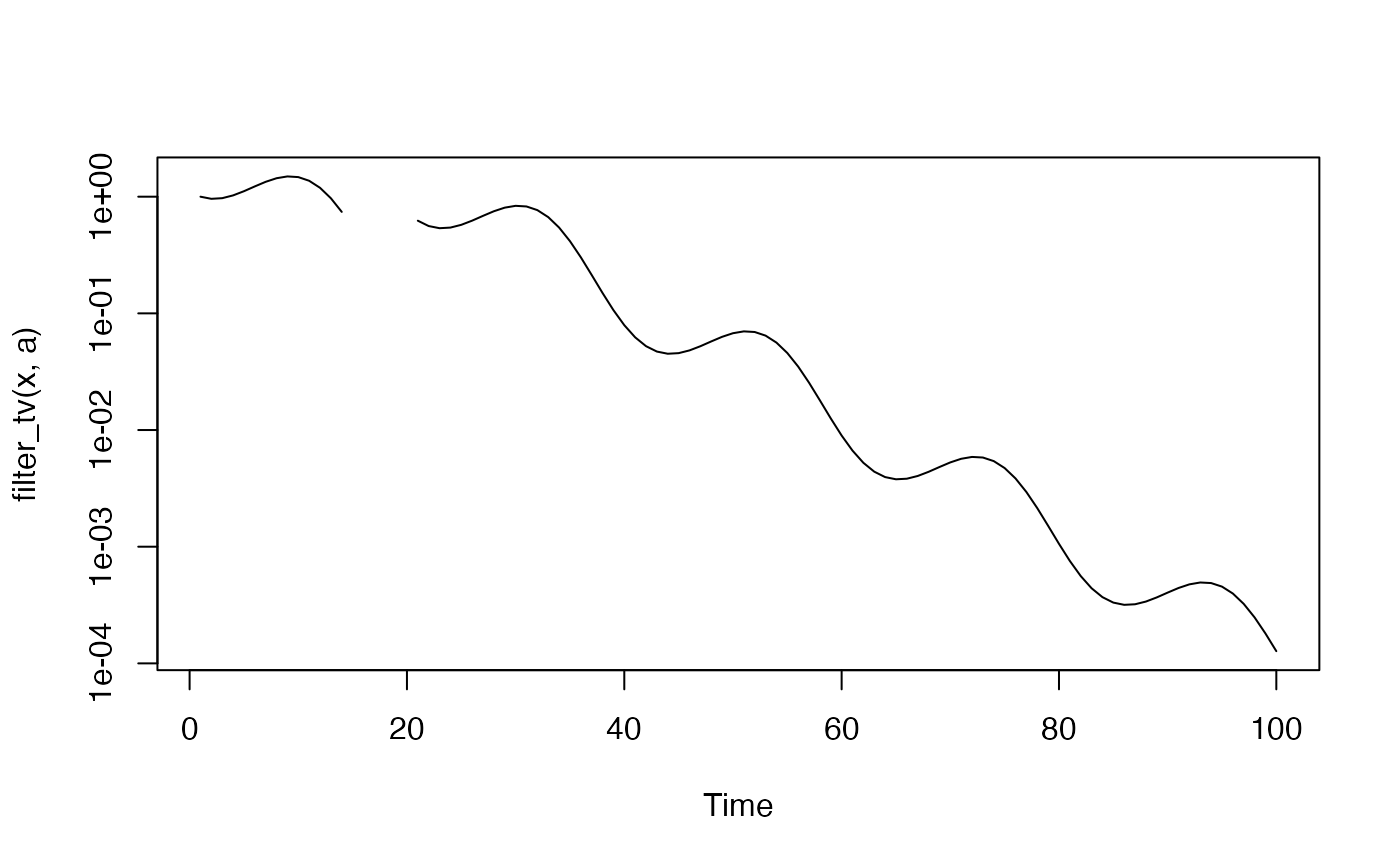
## treatment of missing values
x[15:20] <- NA
plot.ts(filter_tv(x, a), log = "y")
stopifnot(isTRUE(all.equal(y, ftv2(x, a))))
## treatment of missing values
x[15:20] <- NA
plot.ts(filter_tv(x, a), log = "y")