Estimate the dead time between input and output

Use cross-correlation to estimate the delay between an input time series and (rises in) the corresponding output time series.

estimateDelay(
  DATA = data.frame(U = , Q = ),
  rises = TRUE,
  lag.max = hydromad.getOption("max.delay"),
  n.estimates = 1,
  negative.ok = FALSE,
  na.action = na.exclude,
  plot = FALSE,
  main = NULL,
  ...
)

Arguments

DATA

a ts-like object with named components:

list("U"): input (forcing) time series.
list("Q"): output (response) time series.

rises

use only rises in the output to estimate delay.

lag.max

largest delay (in time steps) to consider.

n.estimates

number of estimates of delay to produce.

negative.ok

to allow negative delay times to be considered.

na.action

handler for missing values. The default removes leading and trailing NAs only. Use na.exclude to remove all NAs, but the result will not be a valid autocorrelation sequence.

plot

plot the cross-correlation function.

main

title for plot.

...

further arguments passed to ccf or on to plot.acf.

Value

The estimated delay as an integer number of time steps. If n.estimates > 1, that number of integer delays, ordered by the CCF.

Details

The estimated delay is the one maximising the cross-correlation function.

Author

Felix Andrews felix@nfrac.org

Examples


set.seed(1)
x <- ts(pmax(0, rgamma(200, shape = 0.1, scale = 20) - 5))
## simulate error as multiplicative uniform random
y <- x * runif(200, min = 0.5, max = 1.5)
## and resample 10 percent of time steps
ii <- sample(seq_along(y), 20)
y[ii] <- rev(y[ii])
## apply recursive filter and lag
y <- filter(y, 0.8, method = "r")
y <- lag(y, -2) # true delay is 2
plot(ts.union(y, x))

## based on cross correlation function:
estimateDelay(ts.union(y, x), rises = FALSE, plot = TRUE)

#> [1] 2
## based on ccf with flow rises only:
estimateDelay(ts.union(y, x), plot = TRUE)

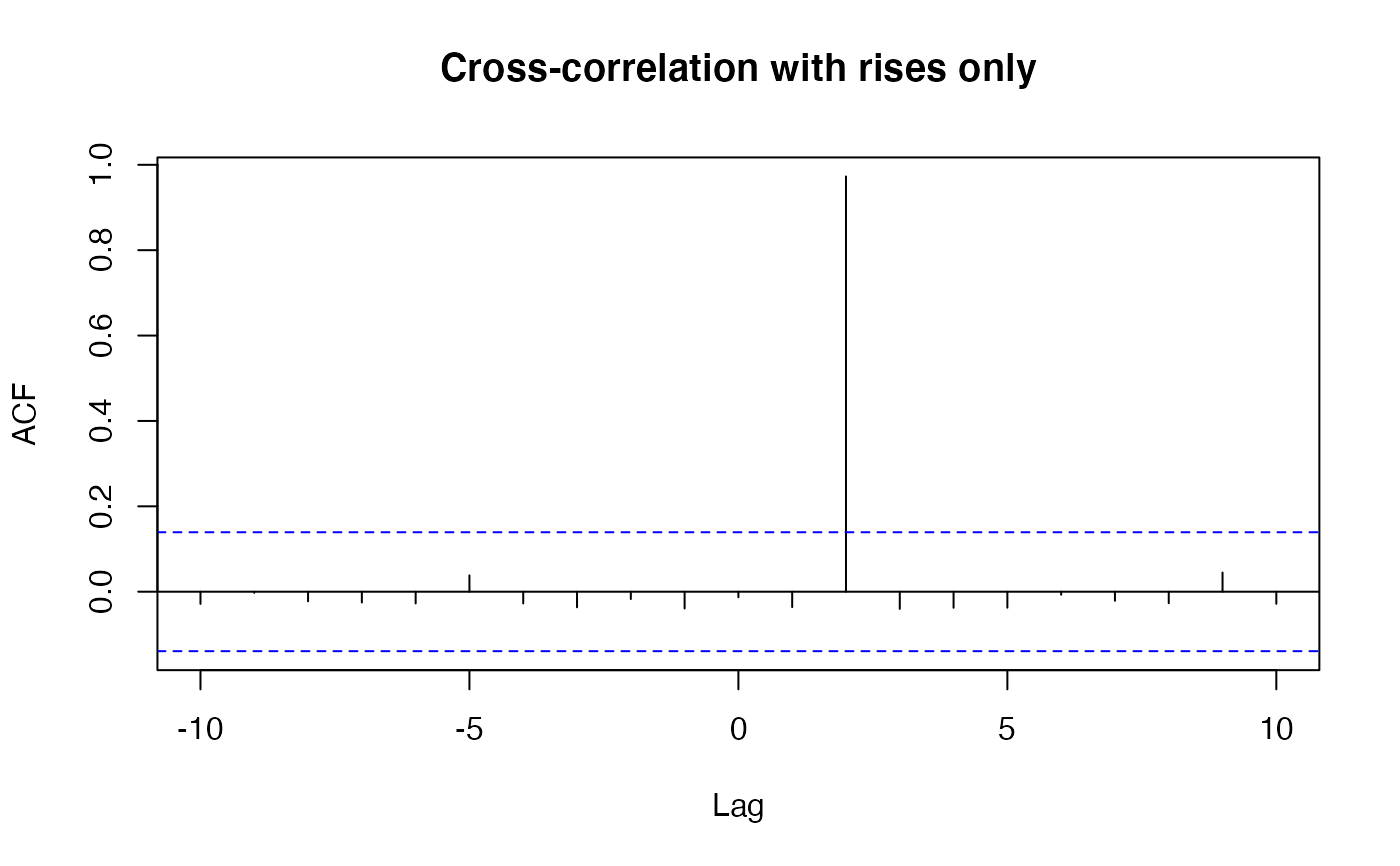#> [1] 2